Уважаемые коллеги. Размещение авторского материала на страницах электронного справочника "Информио" является бесплатным. Для получения бесплатного свидетельства необходимо оформить заявку
Положение о размещении авторского материалаРазмещение информации
Особенности решения задачи единого государственного экзамена на нахождение путей в графе
Графы – замечательные математические объекты, с их помощью можно решать очень много различных, внешне не похожих друг на друга задач. В информатике существуют темы о теории графов, которые изучают графы, их свойства и применение. Первая и главная цель, которую нужно преследовать при изучении графов, научить школьников видеть граф в условии задачи и грамотно переводить условие на язык теории графов.
В едином государственном экзамене по информатике на решение с помощью графа отводиться две задачи (№ 1, 13). Разберём задачу №13 из ДЕМО версии ЕГЭ по информатике 2021 на нахождение путей в графе. Но для начала вспомним, что такое графы и для чего они нужны.
Итак, граф – это не королевское должностное лицо, а абстрактный математический объект, представляющий собой множество вершин графа и набор рёбер, то есть соединение между парами вершин [1] (рисунок 1 «Граф», рисунок 2 «Граф – математический объект»).

Рисунок 1 «Граф»
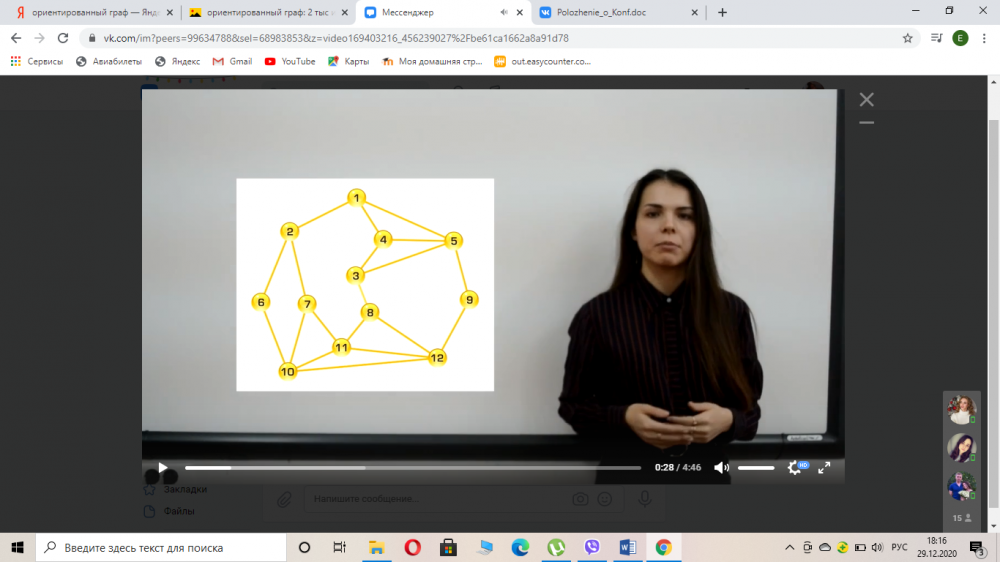
Рисунок 2 «Граф – математический объект»
Многие объекты в нашей жизни могут быть смоделированы при помощи графа. Так например, транспортная схема метрополитена, изображенная в виде станций, соединенных линиями. В терминах графа станции называются вершинами графа, а линии ребра (рисунок 3 «Схема метрополитена»).

Рисунок 3 «Схема метрополитена»
Существуют графы: ориентированные и неориентированные.
Если рёбра графа имеют направление, то оно отображается стрелками, а граф называется ориентированным (направленным). Например, ориентированным будет граф река с притоками. (рисунок 4 «Ориентированный граф»)

Рисунок 4 «Ориентированный граф»
Если вершины или ребра графа характеризуются некоторой дополнительной информацией – весом вершины или ребра, то такой граф называют взвешенным (неориентированным). Например, взвешенным будет граф карта дорог (рисунок 5 «Неориентированный граф»)

Рисунок 5 «Неориентированный граф»
Теперь перейдём к разбору задачи № 13 из Демоверсии ЕГЭ по информатике на подсчёт путей с обязательной вершиной с помощью графа (рисунок 6 «Задание №13»).
Оригинал публикации (Читать работу полностью): Особенности решения задачи единого государственного экзамена на нахождение путей в графе
Назад к списку




