Методические указания к выполнению лабораторной работы «Решение задач линейного программирования в Excel»

Цель: научиться решать задачи линейного программирования в Excel с помощью надстройки «Поиск решения».

 

Краткие теоретические сведения

Оптимизационные задачи находят широкое применение в различных областях практической деятельности: при организации работы транспортных систем, в управлении промышленными предприятиями, при составлении проектов сложных систем. Многие распространенные классы задач системного анализа, в частности, задачи оптимального планирования, распределения различных ресурсов, управления запасами, календарного планирования, межотраслевого баланса укладываются в рамки моделей линейного программирования.

 

Постановка задачи линейного программирования (ЗЛП).

Имеется множество переменных X= (x₁, х₂,..., х_n). Целевая функция линейно зависит от управляемых параметров:

(1)

Имеются ограничения, которые представляют собой линейные формы

где (2)

Требуется определить максимум (минимум) линейной функции

(3)

при условии, что точка (х₁, х₂,..., х_n) принадлежит некоторому множеству D, которое определяется системой линейных неравенств

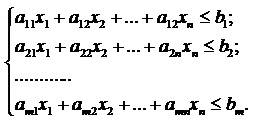(4)

Любое множество значений (х₁*, х₂*,..., х_n*), которое удовлетворяет системе неравенств (4) задачи линейного программирования, является допустимым решением данной задачи. Если при этом выполняется неравенство

c₁х₁^o+ c₂ х₂^o+..+ c_n х_n^o ≥ c₁х₁+ c₂ х₂+..+ c_n х_n

для всего множества значений x₁, х₂,..., х_n, то значение х₁^o..х_n^o является оптимальным решением задачи линейного программирования.

 

Пример построения математической модели и решения ЗЛП.

Задача. Требуется определить, в каком количестве надо выпускать продукцию четырех типов A, B, C иD, для изготовления которой требуются ресурсы трех видов: трудовые, сырье и финансы. Количество ресурса каждого вида, необходимое для выпуска единицы продукции данного типа, называется нормой расхода. Нормы расхода, а также прибыль, получаемая от реализации единицы каждого типа продукции, приведены в таблице1. Там же приведено наличие располагаемого ресурса.

Таблица1.

Ресурс	A	B	C	D	знак	наличие
трудовые	1	1	1	1	≤	16
сырье	6	5	4	3	≤	110
финансы	4	6	10	13	≤	100
прибыль	60	70	120	130	max	-

Составим математическую модель, для чего введем следующие обозначения:

x_i - количество выпускаемой продукции i-го типа, i = 1,2,3,4

b_j –количество располагаемого ресурса j-го вида, j = 1,2,3

a_ji – норма расхода j-го ресурса для выпуска i-ой продукции

c_i – прибыль от реализации единицы продукции i-го типа.

 

Как видно из таблицы 1, для выпуска единицы продукции A требуется 6 единиц сырья, значит, для выпуска всей продукции A требуется 6x₁ единиц сырья, где x₁ - количество выпускаемой продукции A. С учетом того, что для других видов продукции зависимости аналогичны, ограничение по сырью будет иметь вид:

6x₁+ 5x₂+ 4x₃+ 3x₄ ≤ 110

В этом ограничении левая часть равна величине требуемого ресурса, а правая часть показывает количество имеющегося ресурса.

 

Аналогично можно составить ограничения для других видов ресурсов и написать зависимость для целевой функции. Тогда математическая модель задачи будет иметь вид:

x₁+ x₂+ x₃+ x₄ ≤ 16

6x₁+ 5x₂+ 4x₃+ 3x₄ ≤ 110

4x₁+ 6x₂+ 10x₃+ 13x₄ ≤ 100

x_i≥ 0, i=1,2,3,4

1. Для ввода условий задачи создадим форму в Excel (рис.1). В ячейках B3:E3 будут отображаться вычисленные значения x_i.

рис.1. Форма для ввода условий задачи

2. Введем коэффициенты целевой функции и ограничений в форму. Из математической модели введем зависимости. Введенные данные отображены на рис.2.

рис.2. Исходные данные задачи

В ячейке F6 записана формула целевой функции, в F9-F11- левые части ограничений из математической модели. На рис. 3 отображен режим представления формул. Перейти к данному режиму можно с помощью последовательности действий: нажмите кнопку Microsoft Office, щелкните Параметры Excel, откройте вкладку Дополнительно и установите флажок Показывать формулы, а не их значения.

рис.3. Режим представления формул.

3. Загрузим надстройку поиск решения Данные│Анализ│Поиск решения.

4. В поле Установить целевую ячейку введем ссылку на целевую ячейку, для чего установим курсор в поле и щелкнем левой кнопкой мыши по ячейке F6.

5. Выберем направление поиска, установив флажок равной максимальному значению.

6. Установим курсор в поле Изменяя ячейки и введем с помощью мыши имена изменяемых ячеек B3:E3. В этих ячейках в результате поиска решения будет выведено решение – значения переменных x_i., при которых целевая функция имеет максимальное значение при заданных ограничениях.

7. Введем ограничения на искомые переменные: x_i≥0 (нижняя граница по умолчанию равна 0, количество выпускаемой продукции не может быть отрицательным). Так же введем ограничения на ресурсы (не может быть использовано больше ресурсов, чем их запасы). Щелкнем по кнопке Добавить, в появившемся окне Добавление ограничения в левом поле с помощью мыши введем ссылку на ячейку B3, из раскрывающегося списка выберем знак ≥, в правом поле щелкнем мышью по ячейкеB4 (рис.4). Аналогично введем остальные ограничения.

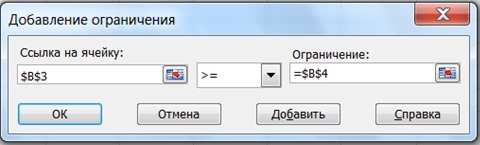
Рис.4. Окно добавления ограничений.

На рисунке 5 показано заполненное окно Поиск решения.

Рис.5 Заполненное окно Поиск решения

8. Далее нажимаем на кнопку Выполнить. Появляется диалоговое окно Результаты поиска решения (рис.6). Решение найдено. Все ограничения и условия оптимальности выполнены. Сохраняем найденное решение. В этом окне также можно получить три вида отчетов: по результатам, устойчивости и пределам, отчеты формируются в новых рабочих листах.

рис.6. Окно Результаты поиска решения

Результаты оптимального решения задачи приведены в таблице (рис.7).

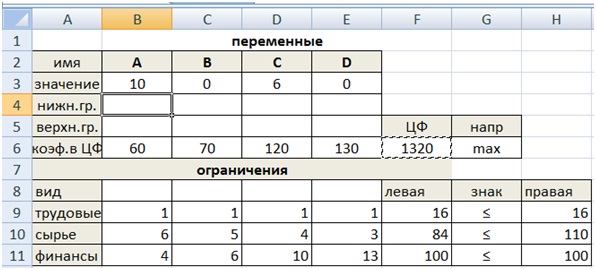
рис.7. Результаты оптимального решения

Таким образом, получилось оптимальное решение (10;0;6;0), т.е. целесообразно выпускать 10 единиц продукции А и 6 единиц продукции С. Максимальная прибыль равна 1320 денежным единицам, при этом используются все трудовые и финансовые ресурсы, 84 единиц сырья, в запасе остается 26 единиц сырья.

 

Задания для лабораторной работы.

Составить математическую модель и решить полученную задачу линейного программирования в Excel с помощью надстройки Поиск решения.

Для перевозки грузов используются машины типов А и Б. Грузоподъемность машин обоих типов одинаковая и равна h т. За одну ходку машина А расходует а₁₁кг смазочных материалов и а₁₂л горючего, машина Б - а₂₁ кг смазочных материалов иа₂₂л горючего. На базе имеется d₁кг смазочных материалов и d₂л горючего. Прибыль от перевозки одной машины А составляет с₁руб., машины Б - с₂руб. Необходимо перевезти H т груза (исходные данные приведены в нижеследующей таблице).

Сколько надо использовать машин обоих типов, чтобы доход от перевозки груза был максимальным.

№ варианта	h	а11	а12	а21	а22	d1	d2	с1	с2	H
0	5	1,5	50	2,0	30	35	900	8	5	100
1	5	1,5	50	2,0	30	45	800	10	7	100
2	5	2,0	40	2,0	40	45	800	8	5	100
3	5	2,0	50	1,5	20	35	900	5	8	200
4	5	1,5	40	2,0	20	35	800	8	5	200
5	10	1,5	30	1,5	30	45	900	7	6	300
6	10	2,0	50	2,0	40	50	1000	10	8	300
7	10	2,0	40	1,5	30	45	800	6	4	200
8	10	1,5	40	1,5	20	35	600	6	5	200
9	10	2,0	45	1,5	30	45	700	8	6	200

 

Инструкция по выполнению лабораторной работы.

1. Изучить теоретический материал.
2. Выполнить приведенный пример.
3. Выбрать свой вариант по последней цифре.
4. Составить математическую модель задачи.
5. Найти оптимальное решение с помощью Поиска решения.
6. Сделать выводы по полученным решениям, сформировать отчеты по результатам решения, устойчивости и пределам.
7. Создать отчет по лабораторной работе.

 

Содержание отчета

1. Титульный лист.
2. Словесная постановка задачи.
3. Математическая формулировка задачи.
4. Заполненное окно Поиск решения
5. Результаты поиска решения (таблица).
6. Выводы по полученным решениям.

 

Список источников

1. Гельман В.Я. Решение математических задач средствами Excel: Практикум. – СПб.:Питер, 2003
2. Курицкий Б.Я. Поиск оптимальных решений средствами Excel. – СПб.: BHV-Санкт-Петербург, 1997
3. Пазюк К.Т. Математические методы и модели в экономике. – Хабаровск: Издательство ХГТУ, 2002
4. Джон Уокенбах. MS OfficeExcel 2007 - Библия пользователя, Издатель: Вильямс, 2008