Методическая разработка урока математики по теме "Системы линейных уравнений и методы их решения"

План урока

Тема урока: Системы линейных уравнений и методы их решения.

Дисциплина: Математика

Специальность: 23.02.03 «Техническое обслуживание и ремонт автомобильного транспорта»

Учебная группа: ТМ-11

Тип урока: комбинированный.

Продолжительность: 90 мин.

Цели:

1. Повторение пройденного материала по теме «Квадратные неравенства».
2. Сформировать понятие системы линейных уравнений.
3. Научить решать системы линейных уравнений способом подстановки, способом сложения, графическим способом.
4. Развитие у студентов рациональных приемов и способов мышления.

Задачи:

1. Формирование умений решать системы линейных уравнений способом подстановки, способом сложения, графическим способом.
2. Развитие познавательной активности, внимания, логики, наблюдательности, самоконтроля.
3. Воспитание самостоятельности интереса к предмету.

Межпредметные связи: информатика.

Комплексно-методическое обеспечение:

• Интерактивная доска
• Учебно-методическое пособие по математике
• Компьютеры

ТЕХНОЛОГИЧЕСКАЯ КАРТА

Приложение 1

1. Решить квадратные неравенства графическим методом:

1. 2х² + 3х -2 > 0
2. 2х² – х – 3 ≤0
3. -2х² +11х – 14 > 0

2. Решить квадратные неравенства методом интервалов:

1. –х² +6х – 9 > 0
2. х² + 8х + 16 < 0
3. –х² + 10х -25 < 0

Приложение 2

Системы линейных уравнений и методы их решения.

1. Понятие системы линейных уравнений.
2. Решение систем линейных уравнений способом подстановки.
3. Способ сложения.
4. Графический способ.

1. Даны два уравнения

     х + у = 12     х – у = 2

Чтобы найти общие решения этих уравнений, требуется решить систему уравнений. Систему уравнений принято записывать с помощью фигурной скобки.

Пара значений переменных х = 7, у = 5 служит решением каждого уравнения системы, так как оба равенства 7+5=12 и 7-5=2 являются верными.

Такую пару чисел называют решением системы.

Решением системы называется пара значений переменных, обращающих каждое уравнение системы в верное равенство.

Решить систему неравенств – научит найти все е решения или доказать, что решений нет.

2. При решении систем линейных уравнений способом подстановки в каком – либо из уравнений системы одно из неизвестных выражается через другое. Полученное выражение подставляется в оставшееся уравнение, после решения которого находится одно неизвестное. Второе неизвестное может быть найдено из любого уравнения системы.  

Пример 1. Решить систему уравнений:

Пример 2. Решить систему уравнений:

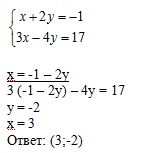
3. При решении систем способом сложения переходим от данной системы к другой, равносильной ей системе, в которой оно из уравнений содержит только одну переменную

Пример 3. Решить систему уравнений:

Пример 4. Решить систему уравнений:

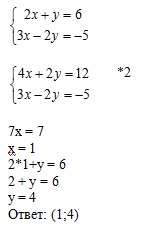
4. Для того, чтобы решить систему линейных уравнений с двумя переменными, можно использовать графики уравнений.

Приложение 3

Задание:

Приложение 4

Задания для самостоятельной работы

Вопросы для самоконтроля

1. Что называют системой линейных уравнений?
2. Как решить систему линейных уравнений способом подстановки?
3. Как решить систему линейных уравнений способом сложения?
4. Как решить систему линейных уравнений графическим способом?

Практические задания:

Задание на «3». Решить системы линейных уравнений:

Задание на «4».

1. Решить систему линейных уравнений способом подстановки:
2. Решить систему линейных уравнений способом сложения:

Задание на «5»:

1. Решить систему линейных уравнений способом подстановки:
2. Решить систему линейных уравнений способом сложения:
3. Решить систему линейных уравнений графическим способом: