Уважаемые коллеги. Размещение авторского материала на страницах электронного справочника "Информио" является бесплатным. Для получения бесплатного свидетельства необходимо оформить заявку
Положение о размещении авторского материалаРазмещение информации
Методическая разработка открытого урока. Обобщающее занятие по теме «Неопределённый и определённый интегралы»
Пояснительная записка
Новое образование состоит в постоянном поиске методов и приёмов созвучных времени, которые так организуют жизнь обучающегося, что в дальнейшем он сможет спокойно, самостоятельно строить свою жизнь. Чем бы наши студенты ни занимались в будущем, хотелось бы видеть их свободными этичными и интеллектуальными личностями. В соответствии с этим желанием я стараюсь строить и стиль диалоговой работы на уроке, и использование математических способностей и достижений студентов при изучении математики. Студенту должно быть интересно на уроке, интерес – это синоним мотивации.
Данный открытый урок был разработан для студентов 2 курса, учитывая основные положения коллективного способа обучения, объяснительно-иллюстративной технологии, технологии взаимного обучения и ИКТ. Раздел «Теория интегрального исчисления» является одним из самых сложных для восприятия разделов математики. Это обусловлено сложностью самого материала, слабо сформированной школьной базой по данному вопросу и ограниченным количеством времени на его изучение на первом и, особенно на втором курсах. На данном уроке студенты подводят итоги изучения темы. Здесь они повторяют, обобщают основные теоретические положения, закрепляют и систематизируют основные методы и приёмы вычисления неопределённого и определённого интегралов, учатся применять знания при решении конкретных практических задач. Целепологание урока проводится через цитирование высказываний великих людей. Ход занятия сопровождается демонстрацией слайдов по каждому этапному моменту урока. В конце урока предлагается тестирование с оригинальной графической самооценкой. Ребята имеют возможность высказать свои впечатления об уроке короткими фразами и пожелания на будущее. Открытый урок рассчитан на 45 минут с дальнейшим его обсуждением.
ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА ПО ДИСЦИПЛИНЕ: МАТЕМАТИКА.
(Специальность: 140102 «Теплоснабжение и теплотехническое оборудование»)
|
Курс, специальность |
2 курс, специальность: 140102 |
||
|
Тема урока |
Обобщающее занятие по теме «Неопределённый и определённый интегралы». |
||
|
Цель урока |
Повторение, систематизация и применение знаний по теме «Неопределённый и определённый интегралы». |
||
|
Задачи урока
|
Обучающие: Повторить, углубить и систематизировать знания, полученные на предыдущих занятиях по данной теме. |
Развивающие: Развивать умения и навыки решать задачи |
Воспитательные: Стремиться к воспитанию навыков вычислительной культуры при решении задач, внимательности, аккуратности и трудолюбия. |
|
Формируемые компетенции |
ОК. 1 |
||
|
Показатели формируемых компетенций |
Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес |
||
|
Средства обучения, оборудование |
Дидактические материалы, доска, мультимедийный проектор, указка лазерная, экран, презентация, лист самооценки, таблица интегралов. |
||
|
Вид учебного занятия |
Теоретическое |
||
|
Применяемые технологии |
Коллективный способ обучения, объяснительно-иллюстративная технология, технология взаимного обучения, ИКТ. |
||
СТРУКТУРА УРОКА
|
ЭТАП 1 (длительность) (2 мин.) |
Организационный момент |
|
Деятельность студентов |
Приветствуют преподавателя и гостей. Записывают тему занятия, слушают установки преподавателя. |
|
Деятельность преподавателя |
Приветствие студентов и гостей, активизация внимания и запись темы занятия, отсутствующие |
|
ЭТАП 2 (длительность) (5 мин.) |
Мотивация. Целевая установка. |
|
Деятельность студентов
|
Зачитывают цитаты, определяют цели и задачи занятия, определяют последовательность действий. Знакомятся с листом самооценки. |
|
Деятельность преподавателя
|
Организовывает целеполагание через цитаты, обосновывает межпредметные связи данной темы с теплотехникой и физикой, формирует алгоритм проведения занятия. Поясняет, как заполнять лист самооценки. |
|
ЭТАП 3 (длительность) (10 мин.) |
Актуализация опорных знаний |
|
Деятельность студентов
|
1. Два студента оформляют решения домашних задач на доске. 2. Фронтальный опрос. 3. Выставляют самооценку за этот этап. |
|
Деятельность преподавателя |
Проводит фронтальный опрос, проверяет правильность решения домашних задач. |
|
ЭТАП 4 (длительность) (10 мин.) |
Обобщение и систематизация знаний (решение задач) |
|
Деятельность студентов |
Поочерёдно выходят к доске решать задачи, подготовленные самостоятельно. Выставляют самооценку. |
|
Деятельность преподавателя |
Следит за правильностью решения задач, отвечает на возникшие вопросы. |
|
ЭТАП 5 (длительность) (5 мин.) |
Применение знаний и умений, в новой ситуации |
|
Деятельность студентов |
Самостоятельная работа (решение нестандартной задачи) |
|
Деятельность преподавателя |
Контролирует правильность выполнения задания |
|
ЭТАП 6 (длительность) (2 мин.) |
Домашнее задание |
|
Содержание домашнего задания |
Задача №1 Вычислить площадь фигуры, ограниченной параболами у = - х2 +8х -5, у = х2 -2х +3. Задача №2 Вычислить площадь фигуры, ограниченной линиями: у = х0,5 у = 0, х = 1, х =9. |
|
ЭТАП 7 (длительность) (5 мин.) |
Контроль усвоения темы (тестирование) |
|
Деятельность студентов |
Выполняют тесты, оценивают их и выставляют самооценку. |
|
Деятельность преподавателя |
Поясняет, как пользоваться тестами, в конце даёт ключи к правильным ответам. |
|
ЭТАП (длительность) (2 мин.) |
Подведение итогов занятия |
|
Деятельность студентов |
Подсчитывают сумму набранных баллов, выставляют оценку за урок. |
|
Деятельность преподавателя |
Выясняет распределение оценок среди студентов за урок. |
|
ЭТАП 8 (длительность) (4 мин.) |
Рефлексия |
|
Деятельность студентов |
Отвечают на вопросы преподавателя по достижению целей, делятся впечатлениями об уроке. |
|
Деятельность преподавателя |
Задаёт вопросы о достижении целей урока, о трудностях, возникших на уроке у студентов. |
ХОД ЗАНЯТИЯ
1. Организационный момент
Здравствуйте ребята, присаживайтесь. Откройте тетради, запишите дату и тему занятия. Занятие № 20. Тема: Обобщающее занятие по теме «Неопределённый и определённый интегралы». Отметим отсутствующих.
2. Мотивация учебной деятельности (Обострить внимание на значимость этой темы, связь её с теплотехникой и другими дисциплинами.)
Определённый интеграл имеет большое практическое применение. С его помощью можно вычислять объёмы и площади поверхностей геометрических тел, длину кривой линии, площади плоских фигур, важные физические величины (работу, силу, теплоту и др.).
Как вы думаете, какое из высказываний, которые вы видите на экране, более всего подходит к теме нашего занятия?
«Недостаточно только получить знания, надо их систематизировать и найти им достойное приложение». Гёте И. (Немецкий поэт и мыслитель18 века.)
«Не в количестве знаний заключается образование, но в полном понимании и искусном применении всего того, что знаешь.» Дистервег А. (Немецкий педагог и политик 19 века.)
«Повторение – мать учения». (Русская народная пословица.)
- Кто бы из вас и выбрал 1 высказывание? Почему?
- Кто бы из вас и выбрал 2 высказывание? Почему?
- Кто бы из вас и выбрал 3 высказывание? Почему?
1-й студент: Мне понравилась пословица. Я считаю, что одной из целей занятия должно быть повторение пройденного материала.
2-й студент: Мне больше понравилось второе высказывание И.Гёте. Я считаю, что нам нужно кроме повторения ещё всё разложить по полочкам, т.е. систематизировать знания и умения.
3-й студент: А я считаю, что все три высказывания подходят к теме нашего занятия, и мы должны сегодня повторять, систематизировать и применять знания на практике.
Вы выбрали все три? И правильно! Значит целью нашего занятия будет: Повторение, систематизация и применение знаний по теме «Неопределённый и определённый интегралы».
Как и в какой последовательности, мы будем достигать эти цели? Что раньше мы будем делать? Писать тест или повторять теорию? Проверять домашнюю работу или выполнять самостоятельную работу? Проводить самоанализ или решать типовые задачи?
Студенты формулируют последовательность действий по достижению целей:
проверим домашнюю работу, повторим теоретический материал, будем решать типовые задачи, напишем тест, проведём самоанализ
Сегодня оценка будет складываться из вашей работы в течении всего занятия.
На столах у вас лежит ЛИСТ САМООЦЕНКИ. Подпишите эти листы Ф.И.О.
|
ЛИСТ САМООЦЕНКИ СТУДЕНТА |
||
|
Ф.И.О |
||
|
Вид оценки (диапазон баллов) |
Пояснения к выставлению баллов |
Количество баллов |
|
Оценка за выполнение домашней работы (0-3б.) |
Правильное решение: 2-х задач –3 балла, 1 задачи - 2 балла, решение задач с ошибками - 1 балл, отсутствие д/з -0 баллов. |
|
|
Оценка за участие во фронтальном опросе ( 0 – 2б.) |
Один правильный ответ – 1 балл, 2 ответа и более - 2 балла.
|
|
|
Оценка за выступление или решение задачи у доски (1б.) |
Одно выступление или решение задачи у доски – 1 балл. |
|
|
Оценка за самостоятельную работу (1б). |
Правильное решение задачи – 1б. |
|
|
Оценка за тестирование (0-5б.) |
За каждый правильный ответ – 1балл. |
|
|
Суммируйте все ваши баллы |
|
|
|
Максимально возможное количество баллов |
12 |
|
|
Если ВЫ набрали (10-12) баллов, поставьте оценку |
5 |
|
|
Если ВЫ набрали (8-9) баллов, поставьте оценку |
4 |
|
|
Если ВЫ набрали (5-7) баллов, поставьте оценку |
3 |
|
|
Если ВЫ набрали (0-4) баллов, поставьте оценку |
2 |
|
|
Ваша оценка |
|
|
3. Актуализация опорных знаний, проверка домашнего задания:
Кто желает оформить на доске своё решение домашних задач? Два студента на доске готовят демонстрацию домашних примеров. Пока ребята готовятся у доски проводится фронтальный опрос. (Вопросы и правильные ответы последовательно высвечиваются на экране в виде слайдов)
1) Что называется первообразной?
2) Что называется неопределённым интегралом?
3) Как обозначается, читается неопределённый интеграл?
4) Что такое интегрирование?
5) Сформулировать 1 свойство неопределённого интеграла.
6) Сформулировать 2 свойство неопределённого интеграла.
7) Сформулировать 3 свойство неопределённого интеграла.
8) Дописать на
доске (наверху) продолжение формулы 
9) Дописать на
доске (наверху) продолжение формулы 
10) Дописать на
доске (наверху) продолжение формулы 
11) Дописать на
доске (наверху) продолжение формулы 
12) Дописать на
доске (наверху) продолжение формулы 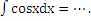
13) Дописать на
доске (наверху) продолжение формулы 
14) Перечислить основные методы интегрирования
15) Как обозначается (читается) определённый интеграл
16) Геометрический смысл определённого интеграла
17) Основные свойства определённого интеграла
18) Дописать на
доске формулу Ньютона – Лейбница 
Слово предоставляем студентам у доски. Выступают студенты с домашними примерами, проверяются их решения, демонстрируются правильные решение на экране, каждый сравнивает своё решение с решением на экране и выставляет самооценку.
Задача № 1 Вычислить
площадь фигуры, ограниченной линиями: у = -х + 8; у = 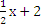 ; у =2. Построим графики
указанных функций в одной системе координат
; у =2. Построим графики
указанных функций в одной системе координат
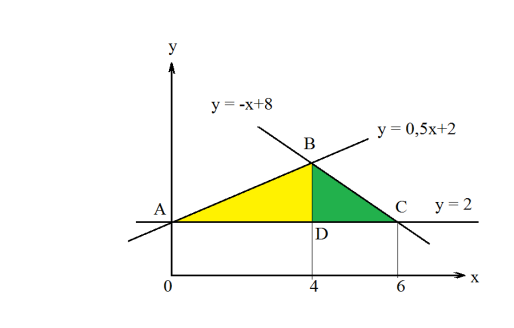
Найдем пределы интегрирования -абсциссы точек
пересечения графиков А,В,С. Для этого решим уравнение: -х + 8 =  т.е ХВ
= 4.
т.е ХВ
= 4. 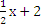 = 2
= 2  т.е ХА=0; -х + 8=2
т.е ХА=0; -х + 8=2  т.е ХС=6. Площадь искомого
т.е ХС=6. Площадь искомого 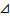 АВС равна сумме площадей
АВС равна сумме площадей 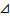 АВD и
АВD и 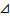 ВСD.
Площади каждого из последних равны разности двух соответствующих определённых интегралов.
ВСD.
Площади каждого из последних равны разности двух соответствующих определённых интегралов.
SABD= 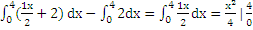 = 4(кв.ед).
= 4(кв.ед).
SBСD= = 2(кв.ед).
= 2(кв.ед).
SАBС =SBСD+SBСD=4+2=6 (кв.ед.). Ответ: 6 кв.ед.
Задача № 2 Вычислить площадь фигуры, ограниченной линиями: у = х2+1; у = - х2+4х +1.
Построим графики указанных функций в одной системе координат

Найдем пределы интегрирования - абсциссы точек
пересечения графиков А и В. Для этого
решим уравнение: х2+1= - х2+4х +1  2х2-4х =0
2х2-4х =0  х(х-2)=0
х(х-2)=0 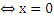 или х=2. Площадь искомой фигуры равна разности
двух определённых интегралов на промежутке [0;2]. S=
или х=2. Площадь искомой фигуры равна разности
двух определённых интегралов на промежутке [0;2]. S= 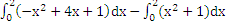 =
= 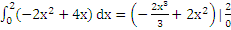 =
=
= ( +8) = 2
+8) = 2 (кв.ед.) Ответ: 2
(кв.ед.) Ответ: 2 кв.единиц.
кв.единиц.
4. Обобщение и систематизация знаний (решение задач)
Приступаем к
решению типовых задач. (Студенты заранее должны приготовить типовые примеры).
А) Метод непосредственного интегрирования. (Вызывают двух студентов для решения интегралов этим методом).
Задача 1: Вычислить интеграл  .
.
Задача 2: Вычислить
интеграл 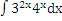
Б) Метод замены
переменной. (Вызывают двух студентов для решения интегралов этим методом). Задача 3: Вычислить интеграл 
Задача 4: Вычислить интеграл 
В) Кто приготовил примеры вычисления интеграла по частям и определённого интеграла? (Вызывают двух студентов для решения этих примеров)
Задача 5 Вычислить
интеграл  .
Напоминается, что метод
интегрирования по частям основан на
формуле:
.
Напоминается, что метод
интегрирования по частям основан на
формуле: 
Задача 6 Вычислить
определённый интеграл 
Напоминается, что определённый интеграл вычисляется по формуле Ньютона –Лейбница:

Те ребята, которые выходили к доске, выставляют баллы за свои решения в лист самооценки
5. Применение знаний и умений, в новой ситуации
Определённый интеграл имеет большое практическое применение (с его помощью можно вычислять объёмы и площади поверхностей геометрических тел, важные физические величины, такие как работу, силу, теплоту и др.). Мы рассмотрим применение определённых интегралов на примере вычисления площади плоской фигуры неправильной формы, где другими способами, точно её вычислить очень сложно. Выполняется небольшая самостоятельная работа (студенты в парах решают задачу №7).
Задача 7: Вычислить площадь земельного участка ограниченного участком параболы
у = - х2+4х и отрезком прямой у = х.
В конце самостоятельной работы на экране демонстрируется правильное решение.
Решение: Построим графики указанных функций в одной системе координат.
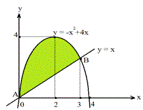
Найдём абсциссы
точек пересечения графиков. Для этого
решим уравнение - х2 +4х=х  -х2 +4х -х=0
-х2 +4х -х=0  - х2 +3х=0
- х2 +3х=0  х(3-х)=0
х(3-х)=0  х=0 или х=3. Площадь искомой фигуры равна
разности площадей двух криволинейных трапеций, а значит разности двух
определённых интегралов на промежутке [0;3].
S=
х=0 или х=3. Площадь искомой фигуры равна
разности площадей двух криволинейных трапеций, а значит разности двух
определённых интегралов на промежутке [0;3].
S=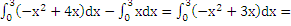
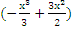 |
| = (-9+27/2) -0 =9/2 = 4,5 (кв.ед).
= (-9+27/2) -0 =9/2 = 4,5 (кв.ед).
Кто правильно решил задачу №7, проставляет самооценку.
6. Пояснение домашнего задания.
Прежде, чем переходить к тестированию, запишите домашнее задание (оно расположено на ваших столах) и посмотрите краткие пояснения к ней на экране.
Задача № 1 Вычислить площадь фигуры, ограниченной параболами
У= - х2+8х -5, у = х2 -2х +3.

Задача №2 Вычислить площадь фигуры, ограниченной линиями: у =  , у = 0, х = 1, х = 9.
, у = 0, х = 1, х = 9.

7. Тестирование
И для закрепления того, что мы с вами прошли, выполним тест по вариантам №1 и №2. Переверните листы самооценки, обнаружите тест. В каждом вопросе выберите правильный ответ и закрасьте ручкой соответствующие кружочки на рисунке. Верхний ряд кружков соответствует ответу «а», средний – «б», нижний – «в». Первый столбец слева соответствует первому вопросу теста и т.д. Затем соедините кружки линией. Поднимите свои работы, и мы увидим улыбки, которые получились на рисунке.
 - Забавная рожица для ответов на вопросы
теста.
- Забавная рожица для ответов на вопросы
теста.
Вариант № 1
1 Вопрос. Выберите правильное продолжение решения: 
а)  б)
б) 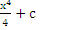 в)
в) 
2 Вопрос. Интегрирование – это действие обратное
а) вычитанию б) дифференцированию в) сложению
3 Вопрос. Чему равен интеграл 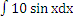
а) = 5cosx +c б)= 2cosx +c в) = -10cosx +c
4 Вопрос.
Написать правильное продолжение формулы 
а)  б)
б) 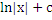 в)
в) 
5 Вопрос. Oпределённый
интеграл 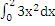 равен:
а) 8 б) 100
в) -20
равен:
а) 8 б) 100
в) -20
Вариант №2
1Вопрос. Выберите правильное продолжение решения:
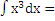 а)
а)  б)
б)  в)
в) 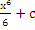
2 Вопрос. Правильность интегрирования можно проверить:
а) сложением б) дифференцированием в) вычитанием
3 Вопрос. Чему равен интеграл 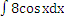
а) = 5sinx +c б)= 2sinx +c в) = 8sinx +c
4 Вопрос. Написать правильное продолжение формулы 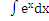 =
=
а)  б)
б)  в) cosx + c
в) cosx + c
5 Вопрос. Oпределённый
интеграл  равен:
а) 1 б) 10 в)
-30
равен:
а) 1 б) 10 в)
-30
Если ответы верные, то получается улыбка, как показано на рисунке.
 Посчитайте
количество верных ответов и заполните листы самооценки. Поставьте оценку за
урок!
Посчитайте
количество верных ответов и заполните листы самооценки. Поставьте оценку за
урок!
8. Рефлексия
Ваши впечатления о занятии
а) Довольны ли вы своими баллами и своей самооценкой?
б) Понравилась ли вам такая форма проведения занятия?
в) Какой этап занятия более всего понравился?
г) Кто из ваших товарищей был на уроке самым активным?
д) Чей ответ больше всего понравился?
Список используемой литературы:
- Богомолов Н.В. Сборник задач по математике для студентов СПО.-М.:Дрофа, 2009.
- Григорьев В.П. Ю.А.Дубинский. Элементы высшей математики. -М.: АСАDEMA,2008.
- Электронный ресурс – режим доступа: http://knowledge.allbest.ru/mathematics
Назад к списку



Ирина
Светлана