Уважаемые коллеги. Размещение авторского материала на страницах электронного справочника "Информио" является бесплатным. Для получения бесплатного свидетельства необходимо оформить заявку
Положение о размещении авторского материалаРазмещение информации
Использование модульной педагогической технологии при изучении тригонометрии
Реформирование образования и внедрение в практику новых педагогических технологий является важнейшим условием интеллектуального, творческого и нравственного развития учащегося в современных условиях. Именно развитие становится ключевым словом педагогического процесса, сущностным, глубинным понятием обучения. Перед учителем на первый план выходит вопрос: «Как сделать так, чтобы урок не только вооружал учащихся знаниями и умениями, значимость которых невозможно оспорить, но чтобы все, что происходит на уроке, вызывало у детей искренний интерес, подлинную увлеченность, формировало их творческое сознание?»
Понятно, что обучение – процесс двухсторонний и для его успеха требуется не только высокое качество работы учителя, но и активная деятельность учащихся, их желание самостоятельно овладевать знаниями. А поскольку весь процесс обучения складывается из отдельных звеньев - уроков, каждый из которых связан со всеми предыдущими в единую цепь, то от правильной организации отдельного урока, грамотного использования различных приемов и методов зависит решение перечисленных выше задач.
Хорошие результаты на уроках математики дает модульная педагогическая технология. Она конструируется на основе ряда целей. Важнейшими из них являются:
- создание комфортного темпа работы каждого ученика,
- определение каждым учеником своих возможностей в учении,
- гибкое построение содержания учебного материала,
- интеграция различных
видов и форм обучения.
Модульное обучение –
альтернатива традиционного обучения, оно интегрирует все то прогрессивное, что
накоплено в педагогической теории и практике. Самым главным отличием модульной технологии
является применение принципа планирования совместной деятельности учителя и
ученика от конечной учебной цели. Опыт использования такой технологии позволяет
сделать вывод, что при обучении создается ситуация успеха для учащихся, что
способствует преодолению страха перед ответом учащихся у доски.
Использование таких
занятий помогает осуществлять индивидуальный подход к учащимся, включать
каждого в осознанную учебную деятельность, мотивировать ее, успешно решать
учебные и коррекционно-развивающие задачи. Эта технология предполагает, как
необходимое условие, формирование
навыков самообучения и самоорганизации, что обеспечивает постепенный переход от
пассивно-воспринимающей позиции к позиции сотрудничества ученика и учителя.
Использование этой технологии способствует основной цели обучения -
саморазвитию учащихся.
При модульном обучении урок должен представлять собой в определенном смысле вполне завершенную и целостную конструкцию.
Это выражается в том, что структура модульного урока, как правило, включает:
• мотивационную беседу (то, что именуется порой организационным моментом или введением в тему урока), завершающуюся постановкой интегрирующей цели урока;
• входной контроль (проверка домашнего задания и повторение изученного ранее);
• работу с новым материалом;
• закрепление изученного;
• завершающий контроль (проверка усвоенного на уроке);
• рефлексию.
Рассмотрим, как можно
организовать некоторые этапы урока по математике на тему «Решение тригонометрических
уравнений различных видов» с использованием данной технологии.
Вот несколько вариантов проведения входного контроля.
1) Индивидуальная работа «Найди ошибку» или «Установи соответствие»
Цель: повторить уровень знаний тригонометрических тождеств.
Эта работа проводится по вариантам.
В первом случае ученикам предлагается таблица формул (таблица № 1), среди которых есть формулы с ошибкой. Ученик должен найти ошибку и записать правильную формулу.
Таблица № 1.
|
Вариант 1. |
Вариант 2. |
|
1. |
1.
cosec x = |
|
2.
sec x = |
2. |
|
3. |
3. |
|
4. |
4. |
|
5. |
5. |
|
6. |
6. |
|
7. |
7. |
|
8. |
8. |
|
9. cos (2 |
9. sin ( |
|
10.
sin ( |
10. cos (
|
|
11.
tg ( |
11. ctg ( |
При втором способе организации работы таблица представляет собой два столбика: в первом записываются левые части некоторых формул, а во втором - правые. При этом количество записей в столбцах должно быть разным. Один из вариантов приведен в таблице № 2.
Таблица № 2.
|
А) tg Б) 1 + ctg2 B) sin Г) Д) сos Е) Ж) З) И) К) tg |
1) cos 2) 3) 1 4) 5) cos ( 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) sin 16) 17) |
2) Работа в парах
Цель: актуализация необходимых знаний по теме для решения заданий на уроке.
Ученики выполняют задания по вариантам, после чего производится взаимопроверка и взаимооценка в парах.
Для этой работы могут, например, использоваться задания, приведенные в таблице № 3.
Таблица № 3.
|
1 вариант |
2 вариант |
|
№1. Запишите формулы для решения простейших тригонометрических уравнений |
|
|
а) sinx = a (1 балл) |
а) cosx = a (1 балл) |
|
б) tgx = a (1 балл) |
б) ctgx = a (1балл) |
|
№2. При каких значениях а эти уравнения имеют решения? (1 балл) |
|
3)Вводный тест, с последующей проверкой в классе.
Цель: проверить уровень умений решения простейших тригонометрических уравнений.
Вводный тест выполняется в рабочих тетрадях учащихся. При этом ребята самостоятельно определяют уровень работы и номер варианта (для уровня А). После выполнения работы они, используя предложенный учителем ключ, проверяют себя и оценивают.
Можно предложить, например, следующие задания для каждого из уровней. Уровень А приведен в таблице № 4.
Таблица № 4
|
1 вариант |
2 вариант |
|
№1. Какие из данных уравнений не имеют корней? (1 балл) |
|
|
а) sinx = - 0,44 |
а) cosx = - 0,33 |
|
б) cosx = 5 |
б) sinx = 4 |
|
в) tgx = - 10 |
в) ctgx = - 8 |
|
г) ctgx = 0 |
г) tgx = 0 |
|
№2. Решите уравнения и выберите верный ответ. |
|
|
А) 2 1) (-1)n arcsin 2) 0 3) – 1 4) нет корней |
А) 2sinx = 1) (-1)n arcsin( 2) 0 3) 1 4) нет корней |
|
Б) 2sinx – 1 = 0 (1 балл) 1) 2) 3) ± 4) (-1)n |
Б) 1 - 2cosx = 0 (1 балл) 1) 2) 3) ± 4) (-1)n |
|
В) sin2x - cos 1) 2) 3) ± 4) (-1)n |
В) tg2x - 2sin 1) 2) 3) ± 4) (-1)n |
|
№3. Найдите корень уравнения на [0; 2cosx = - 1 |
№3. Найдите корень уравнения на [ 2sinx = 1 |
|
№4. Найдите сумму двух наименьших положительных корней уравнения (2б) sinx = - 1 |
№4. Найдите
произведение корней уравнения, принадлежащих промежутку [- сosx = 1/2 |
Уровень Б может содержать следующие задания:
1. Для каких из данных
уравнений число  является
корнем? (2б)
является
корнем? (2б)
А) 2sinx = 0 В) sinx = cosx Б) 3cosx = 0 Д) sinx / (1+cosx) = 0
2. Сколько корней
уравнения tg3x = 1 принадлежат промежутку [0; ]? (3б)
]? (3б)
3. Решите уравнение:
sin( sinx) = - 1.
(3б)
sinx) = - 1.
(3б)
Приведу примеры организации изучения нового материала и его закрепления.
1) Работа в группах
Цель: получение новых знаний в решении различных тригонометрических уравнений
Для организации этого вида работы учитель заранее формирует группы и назначает их лидеров. С лидерами необходимо подробно разобрать решение уравнений различными способами. Каждый лидер самостоятельно должен подготовить к уроку карточки с заданиями для ребят своей группы, проверяя предварительно их правильность у учителя.
В процессе работы задачами лидера являются:
- объяснение ребятам группы способов решения тригонометрических уравнений,
- проверка того, как ребята их поняли, предложив им решить составленные заранее карточки,
- выставление оценок участникам своей группы.
Членам группы можно предложить следующую инструкцию:
1) Внимательно слушайте объяснение лидера группы, фиксируйте в тетради основные моменты решения тригонометрических уравнений.
2) Выполните упражнения, предложенные лидером группы (самостоятельная работа).
3) Проверьте правильность выполнения у лидера группы.
4) Проставь полученную оценку в оценочный лист.
На такой вид работы можно отводить от 15 минут до получаса.
2)Коллективная игра в лото
Цель: закрепление навыка в решении тригонометрических уравнений.
При данной организации работы задания выполняются самостоятельно, ответы обсуждаются в группах разного уровня (группы формируются по желанию самих учащихся). На доске вывешивается таблица с номерами заданий лото.
Раскладываются карточки с различными вариантами ответов. При этом среди них должны быть и неверные ответы, поэтому количество карточек с ответами должно превышать число карточек.
Ученики сами определяют уровень работы: уровень А - простейший, уровень Б - средний, уровень В - самый трудный.
В соответствии с выбранным уровнем заданий они рассаживаются по рядам: 1ряд – уровень А; 2 ряд - уровень Б; 3ряд - уровень В. Первая группа (уровень А) решает задания 1- 4, вторая группа (уровень Б) - задания № 5,6 и третья группа (уровень В) - задания 7,8.
На выполнение заданий обычно достаточно 10 минут. Задания целесообразно раздавать в инструкционных картах.
Сначала ребята работают самостоятельно, затем обсуждают ответы в группе и только после этого проверяют правильность ответов, открывая соответствующие карточки лото. Представитель каждой группы выходит к доске и открывает карточки.
Оценить работу группы по каждому заданию можно по следующим критериям: ответ совпадает полностью - полное количество баллов, указанное в скобках к заданию, ответ совпадает частично - половина указанных баллов, ответ не совпадает - 0 баллов.
При проверке результатов на каждый номер задания накладывается карточка, у которой с одной стороны записан правильный ответ, а с другой - рисунок. Карточки накладываются ответами вниз. Когда на все вопросы будут получены правильные ответы, должно получиться изображение графика непрерывной функции с заданием, а значит, можно переходить к следующему этапу урока. Если же изображение не получилось, то в местах искажения рисунка необходимо проверить соответствующие задания, найти ошибку и только после этого перейти к следующему этапу урока.
Важно помнить, что при модульной технологии урок должен состоять из отдельных элементов. Число элементов может варьироваться от 2-х до 6-и в зависимости от типа урока. При этом каждый элемент должен содержать указания учителя о том, что нужно знать и уметь, или краткие пояснения к выполнению заданий, а также список заданий. Прочитав указания учителя, ученик выполняет самостоятельно задания, которые включены в учебный элемент, и проверяет их по эталонам решений. Эталон учитель демонстрирует ученику, когда тот объявляет о завершении самостоятельной работы. Ученик сравнивает свои ответы с эталонными и исправляет ошибки. Если он получил недостаточное количество баллов, то должен набрать дополнительные баллы в корректирующих заданиях. Для этого ученик решает задания другого варианта, которые аналогичны тем, в которых он допустил ошибку. Вся работа сопровождается оценочным листом учащегося. Оценка за весь модуль зависит от суммы набранных баллов по всем учебным элементам.
В модульную систему обучения хорошо вписываются:
- вся система методов, приемов и форм организации деятельности учащихся,
- работа индивидуальная, в парах, в группах.
Используя модульную технологию, учитель готовится не к тому, как лучше провести объяснение нового, а к тому, как лучше управлять деятельностью учеников. Модульная система обучения дает учителю профессиональный рост, а ученику возможность саморазвития, самореализации. В то же время, эта система обучения требует от учителя большой предварительной работы, а от ученика напряженного труда.
Список литературы:
- Ермаков В.Г. Развивающее образование и функции текущего контроля – Гомель: ГГУ им. Ф.Скорины, 2000
- Левитес Д.Г. Практика обучения: современные образовательные технологии - М.: «Институт практической психологии»,1998
- Селевко Г.К. Современные образовательные технологии: Учебное пособие. – М.: Народное образование, 1998
- Третьяков П.И., Сенновский И.Б. Технология модульного обучения в школе: Практико-оринтированная монография - М.: «Новая школа», 2001
- Чошанов М. A. Гибкая технология проблемно-модульного обучения: Методическое пособие - М.: «Народное образование», 1996
Назад к списку







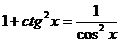

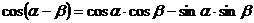



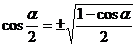

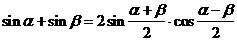

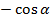
 ) =
) =  ) =
) = 
 ) =
) = )= tg
)= tg 
 )= ctg
)= ctg 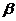 + cos
+ cos =
=


 =
= ctg
ctg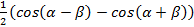


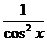

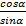




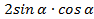


 Z
Z