Игровые технологии на уроках математики. «Что? Где? Когда?» Тема: «Кривые второго порядка»

Продолжаю тему своих публикаций «Дидактические игры при обучении математике». Использование игр на уроках сегодня, в век компьютерных технологий, может показаться не актуальным, но именно в игре даже у взрослого  человека появляется азарт. Кроме того, хочу напомнить, что наука теория вероятностей началась с рассмотрения азартных игр.

Предлагаемые мною игры могут оказать помощь коллегам провести уроки в интересной увлекательной форме, а обучающимся – повысить уровень знаний, умений и навыков и стимулировать интерес к учёбе. В свою очередь, любая игра имеет здоровьесберегающую направленность: снимает физическую и умственную усталость, напряжённость.

Создание даже незначительных игровых ситуаций на уроках  вносит эмоциональную окраску в учебную работу и разнообразие. Игра развивает сообразительность, чувства соревнования, взаимопомощи, различные виды памяти, а самое главное – даёт наибольший эффект в группах, где преобладают обучающиеся с неустойчивым вниманием, пониженным интересом к дисциплине, для которых она – математика - кажется сухой и скучной наукой. В данной публикации я предлагаю вниманию коллег игру «Что? Где? Когда?» и игру «Счастливый случай», в которой используются мультимедийные технологии.

Что? Где? Когда?

Тема: «Кривые второго порядка»

Цель: Расширить знания студентов не только в области математики, развивать познавательный интерес, интеллект, воспитывать стремление к непрерывному совершенствованию своих знаний; формировать дружеские отношения, умение работать командой, показать  межпредметную связь.

Оборудование: Круг, разбитый на сектора; волчок со стрелкой; конверты с вопросами и  указанием номера сектора, одноминутные песочные часы; мелодия к игре; жетоны; чёрный ящик.

Организационный момент

За неделю до игры учитель выбирает команду «Знатоков» и предлагает повторить раздел изученной темы. Остальным учащимся дается задание: составить вопросы для игры (2-3 шт) и сдать их за день до игры. Учитель выбирает наиболее интересные, при Необходимости  корректирует их и складывает в конверты.

Правила игры:

1. Игра состоит из  11 раундов.
2. В каждом раунде знатокам предлагается вопрос из сектора, выпавшего на игровом столе.
3. После обдумывания (3 мин) капитан называет игрока, который будет давать ответ (решения выполняются на доске).
4. Если команда отвечает сразу, то три минуты остается в запасе, и это время дополнительно она может взять в любом раунде.
5. Если команда дает правильный ответ, то ей засчитывается 1 очко. В случае неправильного ответа, может ответить составитель вопроса или кто-то другой, получив при этом жетон.
6. Дважды за игру проводится музыкальная пауза: по объявлению ведущего и по просьбе знатоков.
7. Ведущему (учителю) оказывает помощь один студент: вращает волчок, выносит черный ящик, фиксирует на доске счет игры.

Ход игры

Ведущий:

Есть у меня шестерка слуг,

Проворных и удалых.

И все, что вижу я вокруг,

Все знаю я от них.

Они по знаку моему

Являются в нужде.

Зовут их: Как? И почему?

Кто? Что? Когда? И где?

Р. Киплинг.

Приглашаю игроков занять свои места за игровым столом (представляет игроков, которые по одному занимают свои места).

Примерные вопросы

Сектор №1.

Уважаемые знатоки! Вы, знаете, что 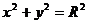 - это каноническое уравнение окружности. Внимание, вопрос: «Какое множество точек на плоскости определяется уравнением 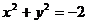 ? Как называется соответствующая кривая второго порядка»?

Сектор №2.

Уважаемые знатоки! Запишите координаты 3^х домов А(7;7), В(8;0) и С(4;-2). Внимание, вопрос: «Где нужно расположить колодец, чтобы он был равноудаленным от каждого из этих домов»?

Сектор №3.

Уважаемые знатоки! Вы изучили кривые второго порядка и знаете, что такое эксцентриситет. Внимание, вопрос: «Чем отличаются эксцентриситеты эллипса, параболы и гиперболы»?

Сектор №4.

Уважаемые знатоки! Обратно пропорциональная зависимость между величинами графически выражаемая равносторонней гиперболой, встречается в различных областях науки и техники. Например, давление Р и объем газа V согласно закону Бойля – Мариотта, связаны обратно-пропорциональной зависимостью РV=С. Внимание, задание: «Составьте каноническое уравнение той ветви равносторонней гиперболы, задаваемой этим соотношением, для которой .»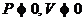

Сектор №5

(Блиц) Уважаемые знатоки! Вам предлагается ответить на три вопроса (по 1 минуте на обдумывание каждого). Очко засчитывается в случае правильного ответа на все 3 вопроса.

Вопрос 1. Эксцентриситеты траекторий движения искусственного спутника земли серии “Космос” и ракеты, отправленной к луне, соответственно равны 0,0045 и 1,05. Определите виды траекторий.

Вопрос 2. Какое слово лишнее в следующем перечне: гипербола, фокус, эксцентриситет, радиус, асимптоты, действительная ось, вершина.

Вопрос 3. Какое множество точек на плоскости определяется уравнением ?

Сектор №6

Уважаемые знатоки! Согласно одному из законов Кеплера, каждая планета Солнечной системы движется по эллиптической траектории, в одном из  фокусов которой находится Солнце. Внимание, вопрос: «Где находится ближайшая к Солнцу точка земной орбиты (перигелий) и наиболее удаленная (афелий)»? (ответ: эти точки являются  вершинами эллипса, лежащими на большой оси).

Сектор №7

Уважаемы знатоки! Три кривые – эллипс, гипербола и парабола – приобрели особенно большое значение после открытий английского ученого Исаака Ньютона, который доказал, что тело под действием  притяжения другого тела может двигаться  либо  по эллиптической, либо по параболической, либо по гиперболической траектории. Внимание, вопрос: «Какие примеры движений по перечисленным траекториям Вы можете привести»? (ответ: эллиптические орбиты планет и спутников; параболические траектории тел, брошенных под углом к горизонту; гиперболические (имеется в виду, конечно, только одна ветвь гиперболы) траектории описывают при движении некоторые кометы Солнечной системы).

Сектор №8.

Внимание! Черный ящик! То, что лежит в черном ящике, изобрел очень талантливый юноша, который придумал гончарный круг, первую в мире пилу. Под пеплом Помпеи археологи обнаружили много таких предметов, изготовленных из бронзы. В нашей стране это было обнаружено при раскопках в Нижнем Новгороде. В Древней Греции умение пользоваться этим предметом считалось верхом совершенства, а уже умение решать задачи с его помощью – признаком высокого положения в обществе и большого ума. Этот предмет незаменим в архитектуре и строительстве. За многие сотни лет конструкция этого предмета не изменилась. В настоящее время им умеет пользоваться любой старшеклассник. Внимание вопрос: «Что лежит в черном ящике»? (ответ: циркуль)

Сектор №9.

Уважаемые знатоки! Провисший между двумя столбами телеграфный провод имеет параболическую форму. Параметр параболы Р=25, а расстояние между столбами 100 м. Внимание, вопрос: «Чему равна наибольшая величина прогиба провода»?  

Сектор № 10

(Супер-блиц). Уважаемые знатоки! Я прошу в этом раунде оставить меня  один на один с одним  из  игроков. Кто из вас продолжит игру?  Три вопроса, на обдумывание каждого игроку дается  не более 30 секунд.

Вопрос 1. Чему равны координаты фокусов F₁и F₂эллипса, заданного уравнением: ?      

Вопрос 2. Куда направлены ветви параболы ?

Вопрос 3. Каким соотношением выражается зависимость между параметрами а, в и с гиперболы?

Сектор №11

Уважаемые знатоки! Задача Дидоны. Финикийская царевна Дидона, спасаясь от своего брата, тирана Пигмалиона, отплыла из родного города Тира. Было это,  если верить легенде, около 825 года до н.э. Долго плавала царевна со своими спутниками по средиземному морю, пока не пристала к берегу Африки. Жили в тех местах нумидийцы. Дидоне место понравилось, и она стала  упрашивать нумидийского царя  Ярба продать ей немного земли. Желая  отделаться от настойчивой царевны, Ярб заломил баснословную цену за клочок земли, который можно окружить только одной бычьей шкурой. К его удивлению Дидона приняла  это издевательское предложение, расплатилась и отправилась отмерять  свою землю, на которой впоследствии основала  великий город  Карфаген. Ярб был в ярости: его одурачили, но он был честным человеком и земля осталась за Дедонорй. Внимание, вопрос: «Как Дидона, имея только одну бычью шкуру, смогла отмерить наибольшую площадь»?

Подведение итогов

1. Ведущий (учитель) Итак, по окончании 11 раундов, счет игры ……. Я  поздравляю команду знатоков с победой и  выставляю им в журнал оценки «5» (Если же игра заканчивается со счетом 5:6 не в пользу  «знатоков», то они  получают оценку «4».

Зрителям, принимавшим участие в составлении вопросов и ответах на них, также выставляются оценки).

2. Встречу в нашем клубе знатоков хочу завершить словами:

Вот уж начался новый век.

По кремнистым ступеням

Взбираясь к опасным вершинам,

Никогда, никогда, никогда

Не отдаст человек

своего превосходства

Умнейшим машинам.

Спасибо всем!