Уважаемые коллеги. Размещение авторского материала на страницах электронного справочника "Информио" является бесплатным. Для получения бесплатного свидетельства необходимо оформить заявку
Положение о размещении авторского материалаРазмещение информации
Дидактическая игра при обучении математике
Подростковый возраст известен как «Возраст пытливого ума, жадного стремления к познанию»…, поэтому дидактические игры вызывают большой интерес. Так как «предмет математики настолько серьёзен, что полезно не упускать случаев делать его немного занимательным», с этой целью, вот уже много лет, я в своей педагогической деятельности использую игровые технологии. В игре появляется возможность многогранного раскрытия личности, развития её способностей, сплочения на основе общих интересов и замыслов.
Своё знакомство с первокурсниками начинаю с игры «Покажи свои знания», которая построена по принципу телепередачи «Своя игра». Обыкновенный вопрос не вызывает должного интереса, кроме того, ребята ещё не знакомы друг с другом, чувствуют себя скованно, неохотно идут на контакт с преподавателем и друг с другом, а потому приходиться очень долго к ним присматриваться, чтобы выявить способности каждого. Наблюдения же во время игры помогают быстро сориентироваться и направить работу в нужное русло.
Ценность игры заключается ещё и в том, что первокурсники обогащаются новыми знаниями с помощью вопросов из истории математики, повторяют пройденный школьный курс, самостоятельно выполняют задания, стараются быть предельно внимательными.
В дальнейшем игры использую на различных этапах урока. Например, при изучении темы «Цилиндр и его свойства» провожу обучающую игру «Конкурс рекламы». Для её проведения накануне, за 3-4 дня, группу делю на две команды – рекламные агентства, назначаю «директоров» и выдаю задание на дом: самостоятельно изучить материал по теме (рекомендую несколько учебников различных авторов) и сделать проект рекламы. Участвуя в подготовке к проведению урока по данной теме, студенты вынуждены приобрести новые знания, а также проявить творческие способности, которые демонстрируются в различных формах выполненных проектов: сказки, частушки, кластеры, презентации, выполненные в программе PowerPoint, видеофильмы…

Например, Высота есть у цилиндра,
А еще – диаметры.
Элементы эти, знайте,
Главные параметры.
Поршень в двигателе есть.
И цилиндр тоже,
А? R?? -
Рассчитать объём поможет.
В процессе усвоения и закрепления новых знаний использую игру «Диалог», направленную на повышение активности студентов. Идея игры состоит в том, что после объявления задания, например, доказать тригонометрическое тождество, создаю ситуацию: сделать это наиболее рациональным способом; студенты стараются наиболее эффективно решить эту проблему. Они понимают, что для её решения понадобится консультация. По правилам игры каждая команда должна задать минимум вопросов с тем, чтобы получить максимум информации. В данной игре я как бы не желаю выдавать информацию, а ребята умело поставленными вопросами вынуждают меня к этому. И если в таком диалоге у них наступает «озарение», значит, задача по развитию творческого мышления выполнена.
Однако при усвоении новых знаний возможности игры значительно уступают традиционным формам обучения. Поэтому игровые занятия провожу чаще всего на повторительно - обощающих уроках при контроле знаний. Например, при изучении стереометрии закрепить пройденный материал и оценить знания студентов помогает игра «Инвентаризация».
В моей педагогической копилке разработана серия коллективных и индивидуальных (настольных) дидактических игр. Каждый из данных видов игр имеет свою педагогическую ценность.
Интеллектуальные настольные игры вызывают у студентов особый интерес. Они применяются на отдельных этапах урока, выступая в виде игровых моментов. Кроме того, настольные игры служат хорошим средством перехода от одной умственной работы к другой.
Коллективные игры позволяют реализовать идеи совместного сотрудничества, соревнования, самоуправления, воспитания через коллектив, приобщения студентов к учебно-научному творчеству, воспитанию ответственности каждого за учёбу и дисциплину в группе, и главную задачу – обучение математике.
В этой статье вниманию коллег предлагаю игру «Инвентаризация» и игру «Брейн – ринг».
Игра – соревнование « Инвентаризация»
Тема: «Поверхности и объемы геометрических тел».
Цель: Активизировать деятельность студентов в процессе обучения; развивать внимание, интуицию, зрительную память, устойчивый интерес к математике.
Оборудование: модели геометрических тел, скатерть, карточки-задания, карточки – ответы.
Организационный момент (правила игры):
Группа делиться на три команды, в каждой из которых имеются студенты со знаниями трех уровней. По ходу игры учитель выставляет каждому студенту баллы, а затем – оценки в журнал. Учет ведется по таблице:
|
Задание |
Команда 1 |
Команда 2 |
Команда 3 |
|
|
Фамилия - балл |
|
|
|
|
|
|
|
|
|
|
|
|
Ход игры
I этап.
На столе находятся модели геометрических тел, накрытые скатертью. Это различного вида призмы, параллелепипеды, пирамиды, конусы, цилиндры шары…
Вызываются к доске по одному человеку от каждой команды (обычно это студенты базового уровня знаний) и предлагается осмотреть набор моделей в течение одной минуты. После осмотра набор моделей вновь накрывается. Играющие должны выполнить «инвентаризацию», то есть записать на доске названия фигур и выполнить от руки их изображения. На составление списка и выполнение изображений отводится 3-5 минут.
II этап.
Затем к доске вызываются следующие участники игры и записывают формулы для вычисления площади поверхности данных фигур.
III этап.
Следующие участники игры записывают формулы для вычисления объемов данных фигур.
IV этап.
Заключительным этапом игры является решение задач трех уровней сложности.
Каждой команде учитель дает 6 карточек – заданий с задачами трех уровней сложности. Игроки распределяют между собой карточки и приступают к решению задач. Задачи базового уровня оцениваются тремя баллами, второго уровня – четырьмя баллами и третьего уровня – пятью баллами.
Итог данного этапа подводится следующим образом: учитель читает задачу, студенты, решающие ее, показывают карточки с полученным ответом (среди карточек с ответами имеются лишние)
Карточки-задания
Карточка 1. (базовый уровень)
Боковая поверхность правильной четырехугольной призмы равна 32 см2, а полная поверхность – 40 см2. Найдите высоту призмы.
(ответ: 4 см)
Карточка 2. (базовый уровень)
Осевое сечение цилиндра – квадрат. Площадь которого равна Q. Найти площадь основания цилиндра.
(ответ:  ).
).
Карточка 3. (II уровень)
В правильной четырехугольной пирамиде определить сторону основания, если боковое ребро равно 5 см, а полная поверхность – 16 см2.
(ответ: 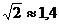 см)
см)
Карточка 4 (II уровень)
Образующая конуса равна 1 и составляет с плоскостью основания угол в 300. Определить объем конуса.
(ответ: 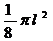 )
)
Карточка 5 (III уровень)
В прямом параллелепипеде стороны основания равны  см и
см и 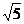 см и образуют угол в 450; меньшая диагональ параллелепипеда равна 7 см. Определить его объем.
см и образуют угол в 450; меньшая диагональ параллелепипеда равна 7 см. Определить его объем.
(ответ: 60 см3)
Карточка 6 (III уровень)
В цилиндре площадь основания равна Q и площадь осевого сечения – М. Определить полную поверхность этого цилиндра.
(ответ: ?М+2Q)
Карточки с ответами



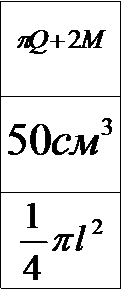
Подведение итогов
1. Определяется команда – победительница по таблице учёта.
2. Выставление оценок всем участникам команды:
· за первое место – оценка 5,
· второе место – 4,
· третье место – оценки поставить выборочно (наивысший балл – 4).
Брейн – ринг
Тема: Итоговый урок
Цель: развивать интерес студентов к более глубокому познанию математики и ее истории, учить логически мыслить, повторить, обобщить и проверить знания за пройденный курс.
Оборудование: на трех столах, покрытых скатертями разного цвета, для трех команд установлены электрические звонки с лампочками, на доске - табло, на столе учителя - гонг.
Правила игры: группа делится на три команды и рассаживается по кругу за тремя столами. Игра проводится в три раунда. Учитель дважды читает задание, затем, произносит слово «время» и ударяет в гонг. После этого команды приступают к выполнению задания. О его готовности команда сообщает звонком, один из игроков отвечает, при необходимости выходит к доске и объясняет, как был получен правильный ответ.
Ход игры
I. Начинается со стихотворения:
Почему торжественно вокруг?
Слышите, как быстро смолкла речь?
Это о царице всех наук
Поведем сегодня с вами речь.
Неслучайно ей такой почет.
Это ей дано давать ответы,
Как хороший выполнить расчет
Для постройки здания, ракеты.
Есть о математике молва,
Что она в порядок ум приводит.
Потому хорошие слова
Часто говорят о ней в народе.
Ты нам, математика, даешь
Для победы трудностей закалку.
Учится с тобою молодежь
Развивать и волю и смекалку.
II. Представление команд друг другу:
- Приветствие
- Девиз
III. Игра
Первый раунд.
Вопросы истории (разыгрываем одно очко)
- При каком царе, впервые русские меры (верста, сажень, аршин, дюйм, фут, пуд, фунт, золотник) были приведены в определенную систему?
(При Петре I)
- Назовите имя самого первого математика
(Фалес Милетцкий)
- Кто из выдающихся русских писателей 14 века окончил физико-математический факультет
(Грибоедов)
- Древнегреческий ученый, изложивший в своих «Началах» первое систематическое построение геометрии реального пространства
(Евклид)
- Как в старину называлось расстояние между концами расставленных большого и указательного пальцев?
(Пядь)
- При каком царе на Руси появляются первые рукописные учебники по математике?
(16 век, Иван Грозный)
- Назовите одно из основных изобретений французского ученого Рене Декарта.
(Координатная плоскость)
- Древние математики Пифагор и Евклид были греками. Неудивительно, что многие термины этой науки у всех народов Европы греческого происхождения. Однако из этих слов имело первоначальное значение «то, что достойно почестей». Затем древние геометры стали называть так положения, не нуждающиеся в доказательствах. Это значение сохранилось в математической терминологии и в наши дни. Что это за слово?
(Аксиома)
- Кто впервые изобрел логарифм?
(Джон Непер)
- «Мантанейн» в переводе с древнегреческого означает – учиться, приобретать знания. Что означает это слово сейчас?
(Математика)
Рекламная пауза
(высказывание о математике (сценка))
Второй раунд.
Вопросы занимательной математики (разыгрываем два очка).
1. Ребята пилят бревна на метровые куски. Отпиливание одного куска занимает одну минуту. За сколько минут распилят бревно длиной 5 метров?
(4 минуты)
2. Однажды в школе учитель предложил классу сложить все числа от 1 до 100, то есть 1+2+3+…..+98+99+100. Пока он диктовал задание у десятилетнего мальчика, Карла Гаусса, впоследствии ставшим великим ученым, королем математики, уже был готов ответ. Назовите его, то есть посчитайте и вы сколько получится?
(5050);
1 2 3………50
100 99 98………51,
т.е. 1+100, 2+99, 3+98….50+51
3. Задача – шутка. Один человек купил трех коз и заплатил три рубля. Спрашивается, по чем каждая коза пошла?
(По траве)
4. В клетке находятся фазаны и кролики. У всех животных 35 голов и 94 ноги. Сколько в клетке кроликов и сколько фазанов?
(12 кроликов и 23 фазана)
5. Как можно одним мешком пшеницы, смолотивши ее, наполнить два мешка, которые столь же велики, как и мешок, в котором находится пшеница?
(Вложить мешок в мешок)
6. Возможно ли такое? Что это может быть: две головы, две руки и шесть ног, а в ходьбе только четыре?
(Всадник на лошади)
7. На какое число надо разделить 2, чтобы получить 4?
(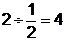 )
)
8.
Понятие «функция» используется в различных науках. Графически можно выразить любую функциональную зависимость. Изобразите в виде графика смысл поговорок: «Чем дальше в лес, тем больше дров». «Выше меры конь не прыгнет).


Музыкальная пауза
(либо кто-то из студентов играет на музыкальном инструменте, если таковых нет, то включить аудиозапись (спокойная музыка)).
Третий раунд
Контрольные вопросы (разыгрываем три очка).
1. Вычислите площадь фигуры, ограниченной линиями:

(ответ:  )
)
2. Что больше 
(ответ:  )
)
3. При вычислении предела вы получили  . Чему это равно? Почему? Ведь делить на 0 нельзя? (
. Чему это равно? Почему? Ведь делить на 0 нельзя? (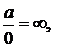 0 – это бесконечно малая величина).
0 – это бесконечно малая величина).
4. Упростите выражение:
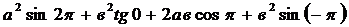
(ответ: -2ав)
5. Найдите корень уравнения: 
(ответ:  )
)
6. Найдите площадь поверхности шара, если его радиус равен значению выражения: 
(ответ: 16?)
7. Запишите в общем виде уравнение прямой, проходящей через начало координат?
(ответ:  )
)
8. Доказать, что 
(ответ: 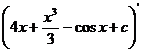 )
)
9. Найдите лишнее по смыслу слово. Остальные слова замените общим названием. Куб, призма, октаэдр, конус, пирамида, параллелепипед, усеченная пирамида.
(Ответ: Конус. Многогранники)
10. Прямые m, n и l пересекаются в одной точке. Через каждые две из них проходит плоскость. Сколько всего различных плоскостей может быть проведено?
(Ответ: через каждые две пересекающиеся прямые проходит 1 плоскость, а всего – три).
III. Итог игры.
1. Награждение победителей дипломами, участников – сертификатами
2. выставление оценок в журнал.
3. Закончить игру песней.
Если тебе одиноко взгрустнется,
Если в твой дом постучится беда,
Если судьба от тебя отвернется,
Песенку эту припомни тогда.
Припев:
Эй, рула-тэ-рула
Тэ-рула, тэ-рула
Тэ-рула – ла – ла
В жизни всему уделяется место,
Рядом с добром уживается зло.
Кто же в турнире хоть раз выступает,
Может считать, что ему повезло.
Припев:
Песенка эта – твой друг и помощник,
Вместе с друзьями ее напевай!
Если от знаний тебя распирает,
Ты свои знанья другим передай
Назад к списку



Ольга Леонидовна
Миронова Татьяна