Обмен опытом

4253

2505

Материалы конференции

197

Работы СНО

1229

Персоналии

251

См. также:

Уважаемые коллеги. Размещение авторского материала на страницах электронного справочника "Информио" является бесплатным. Для получения бесплатного свидетельства необходимо оформить заявку

Положение о размещении авторского материала

Размещение информации

Информационный проект по математике "Магические квадраты"

26.01.2012 14491 1 38809

Кирьянова Олеся Павловна, учитель

МОУ СОШ м-на Вынгапуровский, г. Ноябрьск

Проект выполнила ученица

7в класса Копчук Роксолана

Аннотация

Цель данной работы - выяснить различные варианты составления магических квадратов, изучив которые можно заполнить квадрат любого размера, а так же рассмотреть возможные области их применения.

В ходе работы были использованы следующие методы:

поисковый метод (использование справочной и учебной литературы, а также информационных ресурсов глобальной сети Интернет);
практический метод (составление магических квадратов на основе полученных знаний);
исследовательский метод (составление психологического портрета личности по квадрату Пифагора).

В работе исследуется происхождение и формулируется определение магических квадратов, рассмотрены различные виды квадратов, способы их составления, а так же показана область применения этих загадочных фигур.

В ходе работы над проектом, я не только расширила свои знания по данной теме и повысила свои вычислительные навыки, но и научилась составлять магический квадрат Пифагора, с помощью которого можно познать характер человека, состояние его здоровья, потенциальные возможности, раскрыть достоинства и недостатки.

Во время летних каникул мне часто приходилось решать кроссворды. В одном журнале меня заинтересовала задача на логическое мышление - заполнение магического квадрата. Необходимо было заполнить квадрат числами от 1 до 9 так, чтобы сумма чисел по столбцам, по строкам и по диагоналям была одинакова.

Как это сделать, я не знала, поэтому решила обратиться за помощью к папе. Мы перебирали различные варианты, и, наконец, задача решена. И вот мой квадрат заполнен. Но метод перебора мне не понравился: он отнимает много времени, хотя и позволяет тренировать свои вычислительные навыки. Я предположила, что существует специальный прием, который помогает быстро заполнить магический квадрат. Это и побудило меня заняться данным проектом.

История появления магических квадратов.

Магический квадрат - квадратная таблица из целых чисел, в которой суммы чисел вдоль любой строки, любого столбца и любой из двух главных диагоналей равны одному и тому же числу.

Страна, в которой был впервые придуман магический квадрат, точно неизвестна, неизвестен век, даже тысячелетие нельзя установить точно. Первые упоминания о магических квадратах были у древних китайцев. И, вероятно, самым старым из дошедших до нас магических квадратов является таблица Ло Шу. Она имеет размер 3*3 и заполнена натуральными числами от 1 до 9. В этом магическом квадрате сумма чисел в каждой строке, столбце и диагонали равна 15. Согласно одной из легенд прообразом Ло Шу стал узор из связанных черных и белых точек, украшавший панцирь огромной священной черепахи, всплывшей из вод реки Хуанхэ.

Из Китая магические квадраты распространились сначала в Индию, а затем и в другие страны. В начале XVI века знаменитый немецкий художник Альбрехт Дюрер увековечил магический квадрат в искусстве, изобразив его на гравюре «Меланхолия». Дата создания гравюры (1514 год) указана числами, стоящими в двух центральных клетках нижней строки.

В IX веке. интерес к магическим квадратам вспыхнул с новой силой. Их стали исследовать с помощью методов высшей алгебры. Получение магических квадратов считалось популярным развлечением среди математиков. Ими создавались огромные квадраты, например, 45*45, содержащий числа от 1 до 2025, Были придуманы способы построения магических квадратов любого размера, однако до сих пор не найдена формула, по которой можно было бы найти количество магических квадратов данного размера.

В наше время магические квадраты продолжают привлекать к себе внимание не только специалистов, но и любителей математических игр и развлечений. За последнее столетие значительно возросло число книг по занимательной математике, в которых содержатся головоломки и задачки, связанные с необычными квадратами.

Виды магических квадратов и способы их заполнения.

В ходе своей работы, я пришла к выводу, что магических квадратов 2*2 не существует. Квадрат размером 2*2 должен был бы состоять из чисел 1,2,3,4, а его постоянная была бы равна 5. У такого квадрата по две строки, столбца и диагонали. Чтобы квадрат стал магическим, надо представить число 5 в виде суммы двух данных чисел шестью различными способами, но это сделать не возможно! Ведь таких комбинаций всего две: 1+ 4 и 2+3. Как ни расставляй числа в клетках таблицы, их сумма будет равна 5 либо в каждой строке, либо в обоих столбцах, либо по диагоналям, но никак не одновременно.

Существует единственный магический квадрат 3_*3, так как остальные магические квадраты 3_*3 получаются из него либо перестановкой строк или столбцов либо путем поворота исходного квадрата на 90⁰ или на 180⁰

Общий метод построения квадратов неизвестен. Правила построения магических квадратов делятся на три категории в зависимости от того, каков порядок квадрата. Квадраты могут быть:

- нечетными, то есть состоять из нечетного числа клеток,

- четно-четные, то есть порядок равен удвоенному четному;

- четно-нечетные, то есть порядок равен удвоенному нечетному.

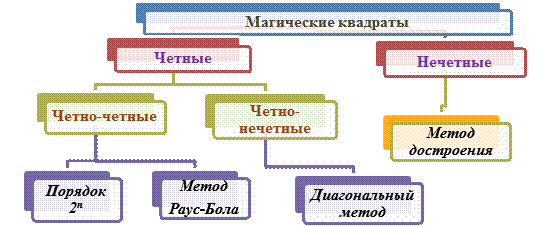
Магические квадраты нечетного порядка.

1. Метод достроения. Рассмотрю на примере квадрата 5*5.

1) Построю квадрат с 25 клетками и временно дострою его до симметричной ступенчатой ромбовидной фигуры. Достроенные клеточки обозначу символом *

			*
		*	*	*

	*				*
*	*				*	*
	*				*

		*	*	*
			*

2) В полученной фигуре располагаю по порядку косыми рядами сверху-вниз-направо 25 целых чисел от 1 до 25.

				1
			6	*	2
		11		7		3
	16		12		8		4
21	*	17		13		9	*	5
	22		18		14		10
		23		19		15
			24	*	20
				25

3). Каждое число, расположенное вне исходного (выделенного) квадрата, следует перенести вдоль того же ряда или столбца ровно на столько клеток от той клетки, которую оно занимает, каков порядок квадрата, в моем примере – на пять.

1 - вниз под 13

2 - вниз под 14

6 - вниз под 18

21 - вправо за 13

22 - вправо за 14

16 - вправо за 8

5 - влево перед 13

4 - влево перед 12

10-влево перед 18

25 - вверх над 13

24 - вверх над 12

20 - вверх над 8

4) Таким образом, все ячейки квадрата заполнены. Сумма чисел в столбцах, строках и диагоналях равна 65.

11	24	7	20	3
4	12	25	8	16
17	5	13	21	9
10	18	1	14	22
23	6	19	2	15

Магические квадраты четно-четного порядка.

1. Порядок 2ⁿ . Этот метод удобно рассматривать на примере магического квадрата 8*8.

1) Исходный квадрат разделю на соответствующее число квадратов порядка 4. В данном случае таких квадратов будет 4. В каждом подквадрате отмечу диагональные элементы символом. Остальные элементы построчно заполню порядковыми целыми числами в направлении слева-направо и сверху-вниз. Числа, приходящиеся на выделенные диагональные элементы, должны быть пропущены.

*	2	3	*	*	6	7	*
9	*	*	12	13	*	*	16
17	*	*	20	21	*	*	24
*	26	27	*	*	30	31	*
*	34	35	*	*	38	39	*
41	*	*	44	45	*	*	48
49	*	*	52	53	*	*	56
*	58	59	*	*	62	63	*

2) Отмеченные * диагональные элементы квадрата заполняю пропущенными целыми числами в порядке возрастания в направлении справа-налево и снизу-вверх, причем числа, приходящиеся на недиагональные элементы, должны быть пропущены.

Сумма чисел по строкам, столбцам и диагоналям равна 260.

64	2	3	61	60	6	7	57
9	55	54	12	13	51	50	16
17	47	46	20	21	43	42	24
40	26	27	37	36	30	31	33
32	34	35	29	28	38	39	25
41	23	22	44	45	19	18	48
49	15	14	52	53	11	10	56
8	58	59	5	4	62	63	1

2. Метод Раус – Бола. Для примера возьму квадрат 8-го порядка.

1) Квадрат заполняется слева направо и сверху вниз числами от 1 до n²в их естественном порядке. Разделить заполненный числами от 1 до 64 квадрат на четыре равных квадрата порядка 4.

1	2	3	4	5	6	7	8
9	10	11	12	13	14	15	16
17	18	19	20	21	22	23	24
25	26	27	28	29	30	31	32
33	34	35	36	37	38	39	40
41	42	43	44	45	46	47	48
49	50	51	52	53	54	55	56
57	58	59	60	61	62	63	64

2) В каждой строке и столбце верхнего левого квадрата порядка 4 отметить 2 (8=2*2*2) клетки (всего 8 клеток). Это можно сделать, применив "шахматный" порядок.

1	2	3	4	5	6	7	8
9	10	11	12	13	14	15	16
17	18	19	20	21	22	23	24
25	26	27	28	29	30	31	32
33	34	35	36	37	38	39	40
41	42	43	44	45	46	47	48
49	50	51	52	53	54	55	56
57	58	59	60	61	62	63	64

3) Для каждой из отмеченных клеток отметить симметричную ей относительно вертикальной оси клетку.

1	2	3	4	5	6	7	8
9	10	11	12	13	14	15	16
17	18	19	20	21	22	23	24
25	26	27	28	29	30	31	32
33	34	35	36	37	38	39	40
41	42	43	44	45	46	47	48
49	50	51	52	53	54	55	56
57	58	59	60	61	62	63	64

4) Содержимое каждой из отмеченных клеток переставить с содержимым соответствующей центрально-симметричной ей клетки. После этих перестановок получится магический квадрат. Сумма его элементов равна 260.

1	63	3	61	60	6	58	8
56	10	54	12	13	51	15	49
17	47	19	45	44	22	42	24
40	26	38	28	29	35	31	33
32	34	30	36	37	27	39	25
41	23	43	21	20	46	18	48
16	50	14	52	53	11	55	9
57	7	59	5	4	62	2	64

Магические квадраты четно-нечетного порядка.

Диагональный метод. Для примера возьму квадрат 10*10.

1) Разделить заполненный числами от 1 до 100 квадрат на четыре квадрата порядка 5 осями симметрии.

1	2	3	4	5	6	7	8	9	10
11	12	13	14	15	16	17	18	19	20
21	22	23	24	25	26	27	28	29	30
31	32	33	34	35	36	37	38	39	40
41	42	43	44	45	46	47	48	49	50
51	52	53	54	55	56	57	58	59	60
61	62	63	64	65	66	67	68	69	70
71	72	73	74	75	76	77	78	79	80
81	82	83	84	85	86	87	88	89	90
91	92	93	94	95	96	97	98	99	100

2) В левом верхнем квадрате закрашу разным цветом три группы клеток, при этом в каждой строке и в каждом столбце отмечу по две клетки из первой группы и по одной — из второй и третьей групп. Одинаковым цветом выделю клетки, расположенные вдоль диагонали квадрата и прямых, ей параллельных.

1	2	33	4	5	6	7	8	9	10
11	12	13	14	15	16	17	18	19	20
21	22	23	24	25	26	27	28	29	30
31	32	33	34	35	36	37	38	39	40
41	42	43	44	45	46	47	48	49	50
51	52	53	54	55	56	57	58	59	60
61	62	63	64	65	66	67	68	69	70
71	72	73	74	75	76	77	78	79	80
81	82	83	84	85	86	87	88	89	90
91	92	93	94	95	96	97	98	99	100

3) Клетки, симметричные клеткам первой группы относительно вертикальной оси, закрашу таким же цветом.

1	2	3	4	5	6	7	8	9	10
11	12	13	14	15	16	17	18	19	20
21	22	23	24	25	26	27	28	29	30
31	32	33	34	35	36	37	38	39	40
41	42	43	44	45	46	47	48	49	50
51	52	53	54	55	56	57	58	59	60
61	62	63	64	65	66	67	68	69	70
71	72	73	74	75	76	77	78	79	80
81	82	83	84	85	86	87	88	89	90
91	92	93	94	95	96	97	98	99	100

4) Число, стоящее в каждой из отмеченных в пункте 2 клеток, переставлю с числом из соответствующей центрально-симметричной клетки.

100	99	3	4	5	6	7	8	92	91
11	89	88	14	15	16	17	83	82	20
21	22	78	77	25	26	74	73	29	30
31	32	33	67	66	65	64	38	39	40
60	42	43	44	56	55	47	48	49	51
50	52	53	54	46	45	57	58	59	41
61	62	63	37	36	35	34	68	69	70
71	72	28	27	75	76	24	23	79	80
81	19	18	84	85	86	87	13	12	90
10	9	93	94	95	96	97	98	2	1

5) Содержимое каждой клетки второй группы обменяю с содержимым симметричной ей относительно горизонтальной оси клетки.

100	99	93	4	5	6	7	8	92	91
11	89	88	84	15	16	17	83	82	20
21	22	78	77	75	26	74	73	29	30
61	32	33	67	66	65	64	38	39	40
60	52	43	44	56	55	47	48	49	51
50	42	53	54	46	45	57	58	59	41
31	62	63	37	36	35	34	68	69	70
71	72	27	28	25	76	24	23	79	80
81	19	18	14	85	86	87	13	12	90
10	9	3	94	95	96	97	98	2	1

6) Содержимое каждой клетки третьей группы обменяю с содержимым симметричной ей относительно вертикальной оси клетки. Получится четно-нечетный магический квадрат с суммой, равной 505.

100	99	93	7	5	6	4	8	92	91
11	89	88	84	16	15	17	83	82	20
30	22	78	77	75	26	74	73	29	21
61	39	33	67	66	65	64	38	32	40
60	52	48	44	56	55	47	43	49	51
50	42	53	54	46	45	57	58	59	41
31	62	63	37	36	35	34	68	69	70
71	72	27	28	25	76	24	23	79	80
81	19	18	14	85	86	87	13	12	90
10	9	3	94	95	96	97	98	2	1

Применение магических квадратов.

Когда я рассмотрела способы составления магических квадратов, меня заинтересовала область их применения. Она показалась мне довольно таки интересной. Сегодня очень актуальным становится вопрос о защите информации. Например, на уроке информатики мы изучали тему кодирование. С помощью магических квадратов так же можно закодировать информацию. Например, зашифровать текст. Расположив буквы согласно числам магического квадрата, получаем фразу «БУДУ В СЕМЬ» или «КЛЮЧИ ПОД КОВРИКОМ».

Так же очень популярна японская головоломка судоку, прародителем которой можно считать Магический квадрат. Она помогает нам развивать логическое мышление и вычислительные навыки. В настоящее время много газет печатают эти головоломки вместе с кроссвордами и другими логическими задачами. Не меньшую популярность завоевали судоку и в сети Интернет.

Англичане используют площадку для игры в шаффлборд, размеченную в виде магического квадрата.

Ну, и, конечно же, в нумерологии. Еще великий ученый Пифагор, считал, что всем на свете управляют числа. Поэтому сущность человека заключается тоже в числе - дате его рождения. Он создал метод построения квадрата, по которому можно познать характер человека, состояние его здоровья и его потенциальные возможности, раскрыть достоинства и недостатки и тем самым выявить, что следует предпринять для его совершенствования. Во времена Пифагора магические квадраты на каждого человека создавались индивидуально. Сейчас есть специальная программа, где вводится дата рождения человека, а на экран выводится готовый магический квадрат. Составлю магический квадрат для себя.

Я родилась 28 июля 1998 года.

1) Складываем числа дня месяца и года рождения, получаем первое рабочее число 44.

2) Далее складываем цифры первого рабочего числа и получаем второе рабочее число 8.

3) Из первого рабочего числа вычитаем удвоенную первую цифру дня рождения, так получается третье рабочее число: 44-(2+2)=40

4) четвертое рабочее число получаем из суммы цифр третьего рабочего числа: 4+0=4

1	4444	7
2	-	888
-	-	99

Теперь выпишу два ряда цифр. Первый состоит из цифр даты рождения: 28.07.1998. Второй - рабочих чисел: 44.8.40.4. Запишу их в квадрат.

«1» – стремлюсь из любого положения извлечь максимальную выгоду, «2» - я человек чувствительный к изменениям в атмосфере, «4444»- у меня отличное здоровье, «7»- для того, чтобы достичь желаемого, я должна много трудиться, «888» – означает, что в жизни, я добьюсь выдающихся результатов, «99»- умна от рождения, знания даются легко.

Чтобы быть более уверенной я использую данный квадрат в качестве талисмана.

Безусловно, не следует слепо верить всему магическому. Возможно, некоторые черты характера и заложены в дате рождения человека, но человек всегда может найти способы что-то изменить в своей судьбе.

Назад к списку

Комментарии

Ошибка в магическом квадрате 10*10. В третьей снизу строке "71 72 27 28 25 76 24 23 79 80" необходимо поменять числа "27" и "28" местами - "28" в третий столбец, и соответственно "27" - в 4-ый. А то сумма по диагонали (слева-вниз) равна 504, в 3-м столбце - 504, а в 4-м - 506.
Чалый Михаил